Models: finer interaction with Cobaya’s pipeline

Interacting with a `model.Model`

During the usual run, what Cobaya’s run() function does internally is using the information in the params, prior, likelihood and theory blocks to create a model.Model, and then have this model interact with a sampler defined in the sampler block (see this diagram).

You can manually create an instance of your model in order to interact with it more finely, e.g.:

Evaluate the prior, likelihood or full posterior at different points of choice
Plot probability along parameter directions
Integrate it into your own pipeline (e.g. write your own sampler)
Extract intermediate quantities (specially useful for complex pipelines, see this example).

To illustrate this, let us revisit the advanced example, in particular when written as a yaml input file

likelihood:
  ring: import_module('my_likelihood').gauss_ring_logp

params:
  r:
    prior: {min: 0, max: 2}
    ref: 1
    proposal: 0.01
    drop: True
  theta:
    prior: {min: 0, max: 1.571}  # =~ [0, pi/2]
    ref: 0
    proposal: 0.5
    latex: \theta
    drop: True
  x:
    value: 'lambda r,theta: r*np.cos(theta)'
    min: 0
    max: 2
  y:
    value: 'lambda r,theta: r*np.sin(theta)'
    min: 0
    max: 2

prior:
  Jacobian: 'lambda r: np.log(r)'
  x_eq_y_band: 'lambda r, theta: stats.norm.logpdf(
      r * (np.cos(theta) - np.sin(theta)), loc=0, scale=0.3)'

sampler:
  mcmc:
    Rminus1_stop: 0.001

output: chains/ring

and a likelihood defined in a separate file my_likelihood.py as

import numpy as np
from scipy import stats


def gauss_ring_logp(x, y, mean_radius=1, std=0.02):
    """
    Defines a gaussian ring likelihood in cartesian coordinates,
    around some ``mean_radius`` and with some ``std``.
    """
    return stats.norm.logpdf(np.sqrt(x**2 + y**2), loc=mean_radius, scale=std)

To create a model, simply call get_model() with your input. You can see below how to create a model and get some log-probabilities from it:

from cobaya.model import get_model

model = get_model("sample_r_theta.yaml")

# Get one random point (select list element [0]).
# When sampling a random point, we need to ignore the Jacobian and
# the gaussian band, since Cobaya doesn't know how to sample from them
random_point = model.prior.sample(ignore_external=True)[0]

# Our random point is now an array. Turn it into a dictionary:
sampled_params_names = model.parameterization.sampled_params()
random_point_dict = dict(zip(sampled_params_names, random_point))
print("")
print("Our random point is:", random_point_dict)

# Let's print some probabilities for our random point
print("The log-priors are:", model.logpriors(random_point_dict, as_dict=True))
print("The log-likelihoods and derived parameters are:",
      model.loglikes(random_point_dict, as_dict=True))
print("The log-posterior is:", model.logpost(random_point_dict))

print("")
print("You can also get all that information at once!")
posterior_dict = model.logposterior(random_point_dict, as_dict=True)
for k, v in posterior_dict.items():
    print(k, ":", v)

This produces the following output:

[model] *WARNING* Ignored blocks/options: ['sampler', 'output']
[prior] *WARNING* External prior 'Jacobian' loaded. Mind that it might not be normalized!
[prior] *WARNING* External prior 'x_eq_y_band' loaded. Mind that it might not be normalized!
[ring] Initialized external likelihood.

Our random point is: {'r': 0.9575006006293434, 'theta': 0.6806752574101642}
The log-priors are: {'0': -1.1448595398334294, 'Jacobian': -0.04342893063840127, 'x_eq_y_band': 0.1737251456633886}
The log-likelihood and derived parameters are: ({'ring': 0.7353357886402638}, {'x': 0.7441196235009879, 'y': 0.6025723077990734})
The log-posterior is: -0.2792275361681782

You can also get all that information at once!
logpost : -0.2792275361681782
logpriors : {'0': -1.1448595398334294, 'Jacobian': -0.04342893063840127, 'x_eq_y_band': 0.1737251456633886}
loglikes : {'ring': 0.7353357886402638}
derived : {'x': 0.7441196235009879, 'y': 0.6025723077990734}

A couple of important things to notice:

Note

Notice that we can only evaluate the posterior at sampled parameters: in the example above, r and theta are sampled (have a prior) but x and y are not (they just act as an interface between the sampler and the likelihood function, that takes cartesian coordinates). So the log-probability methods of model.Model (prior, likelihood, posterior) take (r, theta) but not (x, y).

To get a list of the sampled parameters in use:

print(list(model.parameterization.sampled_params()))

Notice that the log-probability methods of Model can take, as well as a dictionary, an array of parameter values in the correct displayed by the call above. This may be useful (and faster!) when using these methods to interact with external codes (e.g. your own sampler).

Note

0 is the name of the combination of 1-dimensional priors specified in the params block.

Note

If we try to evaluate the posterior outside the prior bounds, logposterior() will return an empty list for the likelihood values: likelihoods and derived parameters are only computed if the prior is non-null, for the sake of efficiency.

If you would like to evaluate the likelihood for such a point, call loglikes() instead.

Note

If you want to use any of the wrapper log-probability methods with an external code, especially with C or Fortran, consider setting the keyword make_finite=True in those methods, which will return the largest (or smallest) machine-representable floating point numbers, instead of numpy’s infinities.

Note

If you had set timing=True in the input info, dump_timing() would print the average computation time of your likelihoods and theory code (see the bottom of section Creating your own cosmological likelihood for a use example).

Note

Notice that, when not called with as_dict=True, the logposterior() method of model.Model produces a model.LogPosterior object, described below, containing the final products of the computation (final here means not intermediate quantities, save for those tracked as derived parameters). For integration into your pipeline, this will be slightly faster, since it has less intermediate steps.

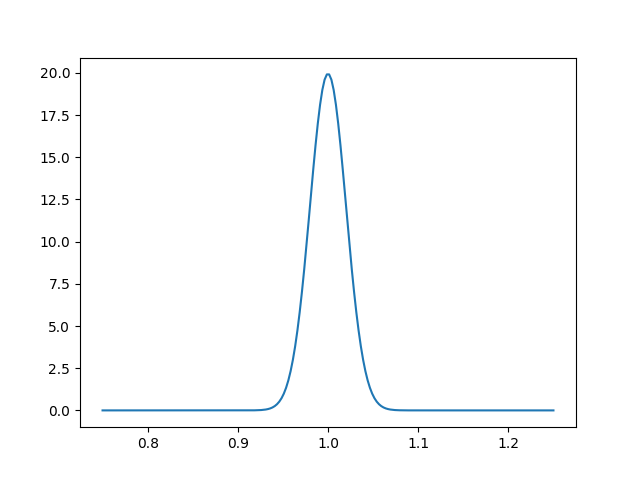
As another example, to plot the value of the likelihood along the radial direction and with theta=pi/4, simply do

import numpy as np
import matplotlib.pyplot as plt
rs = np.linspace(0.75, 1.25, 200)
loglikes = [model.loglike({"r": r, "theta": np.pi / 4}, return_derived=False)
            for r in rs]
plt.figure()
plt.plot(rs, np.exp(loglikes))
plt.savefig('model_slice.png')

Note

Intermediate quantities that are computed as inter-dependencies between different parts of the pipeline, as described in section Creating theory classes and dependencies, can also be obtained from a model. To get them, on the provider attribute of your model.Model instance, use the a get_ method as described in that section.

A practical example of this can be seen in section Using the model wrapper.

Interacting with a sampler

Once you have created a model, you can pass it to a sampler without needing to go through the run() function, which would create yet another instance of the same model (in realistic scenarios this will probably save a lot of time/memory).

You can define a sampler and an optional output driver in the following way:

# Optional: define an output driver
from cobaya.output import get_output
out = get_output(prefix="chains/my_model", resume=False, force=True)

# Initialise and run the sampler (low number of samples, as an example)
info_sampler = {"mcmc": {"max_samples": 100}}
from cobaya.sampler import get_sampler
mcmc = get_sampler(info_sampler, model=model, output=out)
mcmc.run()

# Print results
print(mcmc.products()["sample"])

Conversely, you can also recover the model created by a call to run() from the sampler that it returns:

from cobaya import run
updated_info, sampler = run("sample_r_theta.yaml")
# Here is the model:
model = sampler.model

LogPosterior dataclass

class model.LogPosterior(logpost=None, logpriors=None, loglikes=None, derived=None, finite=False)

Class holding the result of a log-posterior computation, including log-priors, log-likelihoods and derived parameters.

A consistency check will be performed if initialized simultaneously with log-posterior, log-priors and log-likelihoods, so, for faster initialisation, you may prefer to pass log-priors and log-likelhoods only, and only pass all three (so that the test is performed) only when e.g. loading from an old sample.

If finite=True (default: False), it will try to represent infinities as the largest real numbers allowed by machine precision.

make_finite(): Ensures that infinities are represented as the largest real numbers allowed by machine precision, instead of +/- numpy.inf.

as_dict(model)

Given a Model, returns a more informative version of itself, containing the names of priors, likelihoods and derived parameters.

Return type:: Dict[str, Union[float, Dict[str, float]]]

Model wrapper class

model.get_model(info_or_yaml_or_file, debug=None, stop_at_error=None, packages_path=None, override=None)

Creates a model.Model, from Cobaya’s input (either as a dictionary, yaml file or yaml string). Input fields/options not needed (e.g. sampler, output, force, …) will simply be ignored.

Parameters:

info_or_yaml_or_file (Union[InputDict, str, PathLike]) – input options dictionary, yaml file, or yaml text
debug (Optional[bool]) – true for verbose debug output, or a specific logging level
packages_path (Optional[str]) – path where external packages were installed (if external dependencies are present).
stop_at_error (Optional[bool]) – stop if an error is raised
override (Optional[InputDict]) – option dictionary to merge into the input one, overriding settings (but with lower precedence than the explicit keyword arguments)

Return type:

Model

Returns:

a model.Model instance.

class model.Model(info_params, info_likelihood, info_prior=None, info_theory=None, packages_path=None, timing=None, allow_renames=True, stop_at_error=False, post=False, skip_unused_theories=False, dropped_theory_params=None)

Class containing all the information necessary to compute the unnormalized posterior.

Allows for low-level interaction with the theory code, prior and likelihood.

NB: do not initialize this class directly; use get_model() instead, with some info as input.

info()

Returns a copy of the information used to create the model, including defaults and some new values that are only available after initialisation.

Return type:: InputDict

logpriors(params_values, as_dict=False, make_finite=False)

Takes an array or dictionary of sampled parameter values. If the argument is an array, parameters must have the same order as in the input. When in doubt, you can get the correct order as list([your_model].parameterization.sampled_params()).

Returns the log-values of the priors, in the same order as it is returned by list([your_model].prior). The first one, named 0, corresponds to the product of the 1-dimensional priors specified in the params block, and it’s normalized (in general, the external prior densities aren’t).

If as_dict=True (default: False), returns a dictionary containing the prior names as keys, instead of an array.

If make_finite=True, it will try to represent infinities as the largest real numbers allowed by machine precision.

Return type:: Union[ndarray, Dict[str, float]]

logprior(params_values, make_finite=False)

Takes an array or dictionary of sampled parameter values. If the argument is an array, parameters must have the same order as in the input. When in doubt, you can get the correct order as list([your_model].parameterization.sampled_params()).

Returns the log-value of the prior (in general, unnormalized, unless the only priors specified are the 1-dimensional ones in the params block).

If make_finite=True, it will try to represent infinities as the largest real numbers allowed by machine precision.

Return type:: float

loglikes(params_values=None, as_dict=False, make_finite=False, return_derived=True, cached=True)

Takes an array or dictionary of sampled parameter values. If the argument is an array, parameters must have the same order as in the input. When in doubt, you can get the correct order as list([your_model].parameterization.sampled_params()).

Returns a tuple (loglikes, derived_params), where loglikes are the log-values of the likelihoods (unnormalized, in general) in the same order as it is returned by list([your_model].likelihood), and derived_params are the values of the derived parameters in the order given by list([your_model].parameterization.derived_params()).

To return just the list of log-likelihood values, make return_derived=False (default: True).

If as_dict=True (default: False), returns a dictionary containing the likelihood names (and derived parameters, if return_derived=True) as keys, instead of an array.

If make_finite=True, it will try to represent infinities as the largest real numbers allowed by machine precision.

If cached=False (default: True), it ignores previously computed results that could be reused.

Return type:: Union[ndarray, Dict[str, float], Tuple[ndarray, ndarray], Tuple[Dict[str, float], Dict[str, float]]]

loglike(params_values=None, make_finite=False, return_derived=True, cached=True)

Takes an array or dictionary of sampled parameter values. If the argument is an array, parameters must have the same order as in the input. When in doubt, you can get the correct order as list([your_model].parameterization.sampled_params()).

Returns a tuple (loglike, derived_params), where loglike is the log-value of the likelihood (unnormalized, in general), and derived_params are the values of the derived parameters in the order given by list([your_model].parameterization.derived_params()). If the model contains multiple likelihoods, the sum of the loglikes is returned.

To return just the list of log-likelihood values, make return_derived=False, (default: True).

If make_finite=True, it will try to represent infinities as the largest real numbers allowed by machine precision.

If cached=False (default: True), it ignores previously computed results that could be reused.

Return type:: Union[float, Tuple[float, ndarray]]

logposterior(params_values, as_dict=False, make_finite=False, return_derived=True, cached=True, _no_check=False)

Takes an array or dictionary of sampled parameter values. If the argument is an array, parameters must have the same order as in the input. When in doubt, you can get the correct order as list([your_model].parameterization.sampled_params()).

Returns a LogPosterior object (except if as_dict=True, see below), with the following fields: :rtype: Union[LogPosterior, dict]

logpost: log-value of the posterior.
logpriors: log-values of the priors, in the same order as in list([your_model].prior). The first one, corresponds to the product of the 1-dimensional priors specified in the params block. Except for the first one, the priors are unnormalized.
loglikes: log-values of the likelihoods (unnormalized, in general), in the same order as in list([your_model].likelihood).
derived: values of the derived parameters in the order given by list([your_model].parameterization.derived_params()).

Only computes the log-likelihood and the derived parameters if the prior is non-null (otherwise the fields loglikes and derived are empty lists).

To ignore the derived parameters, make return_derived=False (default: True).

If as_dict=True (default: False), returns a dictionary containing prior names, likelihoods names and, if applicable, derived parameters names as keys, instead of a LogPosterior object.

If make_finite=True, it will try to represent infinities as the largest real numbers allowed by machine precision.

If cached=False (default: True), it ignores previously computed results that could be reused.

logpost(params_values, make_finite=False, cached=True)

Takes an array or dictionary of sampled parameter values. If the argument is an array, parameters must have the same order as in the input. When in doubt, you can get the correct order as list([your_model].parameterization.sampled_params()).

Returns the log-value of the posterior.

If make_finite=True, it will try to represent infinities as the largest real numbers allowed by machine precision.

If cached=False (default: True), it ignores previously computed results that could be reused.

Return type:: float

get_valid_point(max_tries, ignore_fixed_ref=False, logposterior_as_dict=False, random_state=None)

Finds a point with finite posterior, sampled from the reference pdf.

It will fail if no valid point is found after max_tries.

If ignored_fixed_ref=True (default: False), fixed reference values will be ignored in favor of the full prior, ensuring some randomness for all parameters (useful e.g. to prevent caching when measuring speeds).

Returns (point, LogPosterior(logpost, logpriors, loglikes, derived))

If logposterior_as_dict=True (default: False), returns for the log-posterior a dictionary containing prior names, likelihoods names and, if applicable, derived parameters names as keys, instead of a LogPosterior object.

Return type:: Union[Tuple[ndarray, LogPosterior], Tuple[ndarray, dict]]

dump_timing()

Prints the average computation time of the theory code and likelihoods.

It’s more reliable the more times the likelihood has been evaluated.

add_requirements(requirements): Adds quantities to be computed by the pipeline, for testing purposes.

requested()

Get all the requested requirements that will be computed.

Returns:: dictionary giving list of requirements calculated by each component name

get_param_blocking_for_sampler(split_fast_slow=False, oversample_power=0)

Separates the sampled parameters in blocks according to the component(s) re-evaluation(s) that changing each one of them involves. Then sorts these blocks in an optimal way using the speed (i.e. inverse evaluation time in seconds) of each component.

Returns tuples of (params_in_block), (oversample_factor), sorted by descending variation cost-per-parameter.

Set oversample_power to some value between 0 and 1 to control the amount of oversampling (default: 0 – no oversampling). If close enough to 1, it chooses oversampling factors such that the same amount of time is spent in each block.

If split_fast_slow=True, it separates blocks in two sets, only the second one having an oversampling factor >1. In that case, the oversampling factor should be understood as the total one for all the fast blocks.

check_blocking(blocking)

Checks the correct formatting of the given parameter blocking and oversampling: that it consists of tuples (oversampling_factor, (param1, param2, etc)), with growing oversampling factors, and containing all parameters.

Returns the input, once checked as (blocks), (oversampling_factors).

If draggable=True (default: False), checks that the oversampling factors are compatible with dragging.

set_cache_size(n_states)

Sets the number of different parameter points to cache for all theories and likelihoods.

Parameters:: n_states – number of cached points

get_auto_covmat(params_info=None)

Tries to get an automatic covariance matrix for the current model and data.

params_info should include the set of parameters for which the covmat will be searched (default: None, meaning all sampled parameters).

measure_and_set_speeds(n=None, discard=1, max_tries=inf, random_state=None)

Measures the speeds of the different components (theories and likelihoods). To do that it evaluates the posterior at n points (default: 1 per MPI process, or 3 if single process), discarding discard points (default: 1) to mitigate possible internal caching.

Stops after encountering max_tries points (default: inf) with non-finite posterior.

Models: finer interaction with Cobaya’s pipeline

Interacting with a model.Model

Interacting with a sampler

LogPosterior dataclass

Model wrapper class

Interacting with a `model.Model`